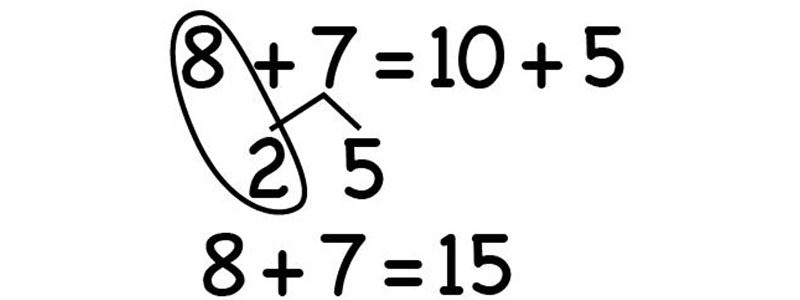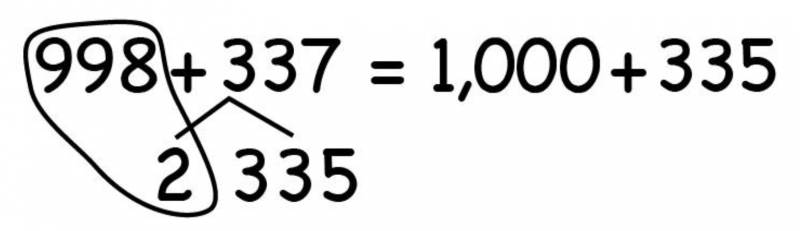Kids need multiple strategies to succeed in math class. How the number bond can be a powerful alternative to ‘just adding’
LauraMarie Coleman | November 18, 2019
Your donation will help us produce journalism like this. Please give today.
 “Why can’t we just teach kids to add numbers anymore? It seems like 2 + 2 doesn’t equal 4 these days.”
“Why can’t we just teach kids to add numbers anymore? It seems like 2 + 2 doesn’t equal 4 these days.”
As an educator, I have encountered this conversation in parent-teacher conferences, with my chiropractor, and numerous times at parties and on airplanes, to name just a few occasions.
People want to know why students need to do so many extra steps and learn multiple strategies for solving problems. Some suggest that simply learning the standard algorithm for a math problem (2 + 2 = 4, 6 x 8 = 48, etc.) is enough; kids just need to arrive at the correct answer.
Yes, students need to learn the rules and procedures for doing calculations. In some cases, that’s the best tool for the job.
But students also need options — more tools in their toolbox and conceptual understanding that helps them pick the best tool. Just as a carpenter would never show up at a worksite with only a hammer, students need a range of tools and strategies for their classwork.
Consider the following problem:
To solve 998 + 337 using the traditional method, students must learn a complex series of steps. First, add 8 and 7 to get 15. Put the 5 at the bottom and carry the 1. Then, add 9 and 3 plus the extra 1. Write the 3 at the bottom and carry the 1. Finally, add the next 9 and 3 plus the extra 1 on top again. Then, write the 13 at the bottom.
This process sets students on the path to the correct answer, but it uses language totally disconnected from any conceptual understanding. Besides, have you ever stood in a store trying to add numbers up using this method, writing in the air with your finger like an imaginary pencil as you visualize each of these steps? Does this feel effective or efficient in that moment?
Using a model called number bonds makes this problem simple.
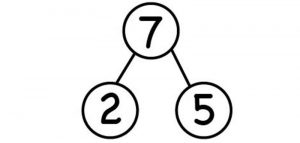
To use this model, first, students have to learn that all numbers can be made up of different parts. For example, that 7 can be broken apart into 2 and 5.
Then, students can use those parts to make an easier problem. If they understand the properties of addition and know that they can break apart the numbers and put them back together in groups that are easier to add in their head, they can see that 7 + 8 is the same as 10 + 5. This is an easy mental math problem.
Once students understand the concept of number bonds and how to use them in computation, they can quickly solve more complex problems, such as 998 + 337. As above, the first step is to make 998 a friendlier number. Notice that 998 is almost 1,000; it just needs 2. We can get the 2 from 337 by using a number bond. When we break apart 337 and one part is 2, the other part is 335.
The two numbers are now 1,000 and 335, which even young students can quickly add to get 1,335, the same sum as 998 + 337. This method is faster and has fewer opportunities for computational mistakes.
Both the standard algorithm and number bonds can get students to the correct answer. The question is: Are we looking to create math robots who simply follow the steps to get the answer, or human beings who can apply what they know to life and accurately do math without pencil and paper or a calculator?
The truth is, when you really have this conversation with adults, you find that many of us use number bonds or similar strategies. We just never knew they had a name and that this is what they might look like on paper. Adults today never had the benefit of someone teaching us this strategy. We had to figure it out on our own.
Luckily, a growing number of students now have access to good educational standards, modern curriculum and teachers who can help.
LauraMarie Coleman works with and coaches teachers on professional development for Great Minds. Previously, she was a special education classroom teacher and an instructional coach, working with alternative and special education students and teachers in grades K-8 in Binghamton, New York.